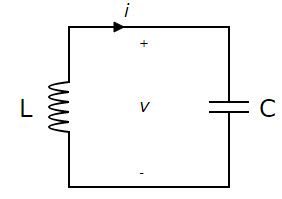
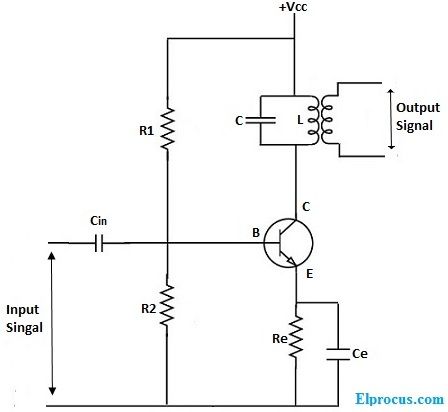
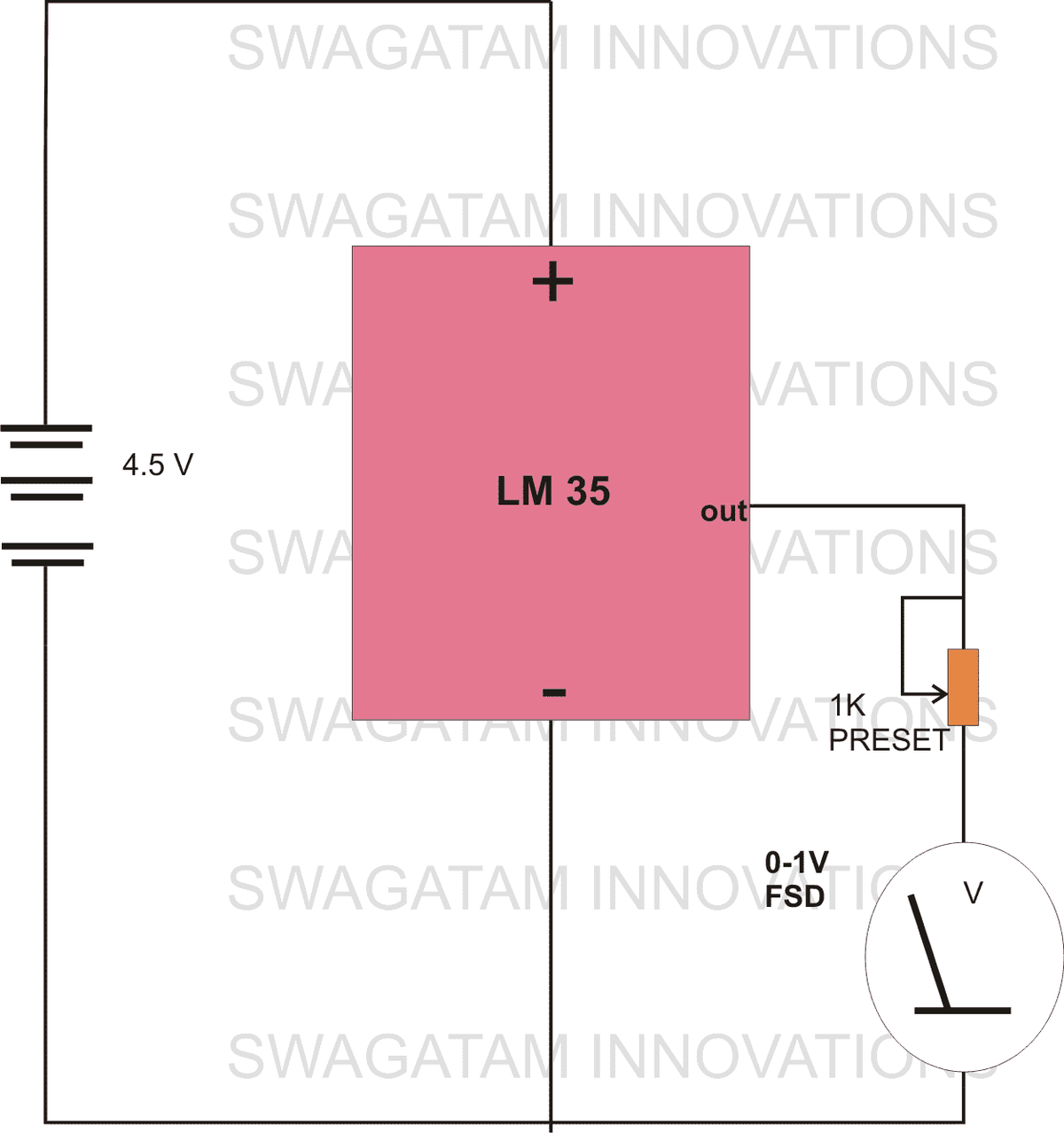
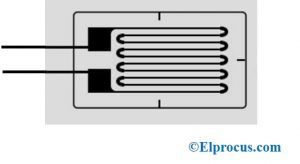
Plik Twierdzenie o maksymalnym przenoszeniu mocy można zdefiniować jako obciążenie rezystancyjne jest podłączone do sieci DC, gdy rezystancja obciążenia (R._L) jest równoważny rezystancji wewnętrznej, wtedy otrzymuje najwyższą moc, znaną jako równoważna rezystancja sieci źródłowej Thevenina. Twierdzenie określa, jak wybrać rezystancję obciążenia (RL), gdy rezystancja źródła jest podana raz. Stosowanie twierdzenia w odwrotnej sytuacji jest nieporozumieniem. Nie oznacza to, że jak wybrać rezystancję źródła dla określonej rezystancji obciążenia (RL). W rzeczywistości rezystancja źródła, która najlepiej wykorzystuje przenoszenie mocy, jest stale zerowa, poza wartością rezystancji obciążenia. To twierdzenie można rozszerzyć do AC obwody które zawierają reaktancję i określają, że najwyższa transmisja mocy ma miejsce, gdy impedancja obciążenia (ZL) musi być równoważna ZTH (sprzężenie zespolone o odpowiedniej impedancji obwodu).

Twierdzenie o maksymalnym przenoszeniu mocy

Twierdzenie o przenoszeniu maksymalnej mocy rozwiązane

Znajdź rezystancję obciążenia RL, która umożliwia obwodowi (po lewej stronie zacisków a i b) dostarczenie maksymalnej mocy w kierunku obciążenia. Znajdź również maksymalną moc dostarczaną do obciążenia.

Przykład twierdzenia o przenoszeniu maksymalnej mocy

Rozwiązanie:

Aby zastosować twierdzenie o maksymalnym przenoszeniu mocy, musimy znaleźć obwód zastępczy Thevenina.

a) V wyprowadzenie obwodu: otwarty obwód Napięcie

napięcie otwartego obwodu

Ograniczenia: V1 = 100, V2 - 20 = Vx i V3 = Vth

W węźle 2:

W węźle 3:

(1) * 2 + (2) * 3 -> Vth = 120 [V]

(b) Wyprowadzenie Rth (metodą testowania napięcia): Po dezaktywacji i teście zastosowanie napięcia , mamy:

Po dezaktywacji i podaniu napięcia testowego

Ograniczenia: V3 = VT i V2 = Vx

W węźle 2:

W węźle 3 (KCL):

Od (1) i (2):

Obwód wyników

Aby uzyskać maksymalny transfer mocy, RL = 3 = Rth. Wreszcie maksymalna moc przenoszona do RL wynosi:

Określ maksymalną moc, jaką można dostarczyć do rezystor zmienny R.

Twierdzenie o przenoszeniu maksymalnej mocy Przykład 2

Rozwiązanie:

(a) Vth: napięcie w obwodzie otwartym

Vth_ Napięcie otwartego obwodu

Z obwodu Vab = Vth = 40-10 = 30 [V]

(b) Rth: Zastosujmy metodę rezystancji wejściowej:

Rth_ Zastosujmy metodę rezystancji wejściowej

Wtedy Rab = (10 // 20) + (25 // 5) = 6,67 + 4,16 = 10,83 = Rth.

Obwód Thevenina

Formuła twierdzenia o przenoszeniu maksymalnej mocy

Jeśli weźmiemy pod uwagę η (sprawność) jako ułamek mocy rozpuszczonej przez obciążenie R do mocy rozszerzonej o źródło, VTH , to można łatwo obliczyć wydajność jako

η = (Pmax / P) X 100 = 50%

Gdzie maksymalna moc (Pmax)

Pmax = V^dwa_THR_{TH / (}R_{TH +}R_TH)dwa₌V^dwa_{TH /}4R_TH

A dostarczana moc (P) jest

P = 2 V.^dwa_{TH /}4R_TH= V^dwa_TH/ 2r_TH

Η wynosi tylko 50%, gdy osiągany jest najwyższy transfer mocy, chociaż osiąga 100% jako R_L(rezystancja obciążenia) osiąga nieskończoność, podczas gdy cały stopień mocy dąży do zera.

Twierdzenie o przenoszeniu maksymalnej mocy dla obwodów prądu przemiennego

Podobnie jak w układzie aktywnym, największa moc jest przenoszona do obciążenia, podczas gdy impedancja obciążenia jest równoważna złożonemu sprzężonemu odpowiadającej impedancji danego zestawu, obserwowanej na zaciskach obciążenia.

Twierdzenie o maksymalnym przenoszeniu mocy dla obwodów prądu przemiennego

Powyższy obwód jest odpowiednikiem obwodu Thevenina. Gdy powyższy obwód zostanie rozważony na zaciskach obciążenia, wówczas przepływ prądu zostanie podany jako

I = VTH / ZTH + ZL

Gdzie ZL = RL + jXL

ZTH = RTH + jXTH

W związku z tym,

I = VTH / (RL + jXL + RTH + jXTH)

= VTH / ((RL + RTH) + j (XL + XTH))

Moc przekazana do obciążenia,

PL = I2 RL

PL = V2TH × RL / ((RL + RTH) 2 + (XL + XTH) 2) …… (1)

Dla największej mocy pochodna powyższego równania powinna wynosić zero, później niż w uproszczeniu otrzymamy następujący.

XL + XTH = 0

XL = - XTH

Zastąp wartość XL w powyższym równaniu 1, a następnie otrzymamy następujący.

PL = V2TH × RL / ((RL + RTH) 2

Ponownie, aby przenieść największy transfer mocy, powyższe wyprowadzenie równania musi być równoważne zeru, po rozwiązaniu tego możemy otrzymać

RL + RTH = 2 RL

RL = RTH

Dlatego największa moc będzie przesyłana ze źródła do obciążenia, jeśli RL (rezystor obciążenia) = RTH i XL = - XTH w obwodzie prądu przemiennego. Oznacza to, że impedancja obciążenia (ZL) musi być równoważna ZTH (sprzężenie zespolone o odpowiedniej impedancji obwodu)

ZL = ZTH

Ta maksymalna przenoszona moc (Pmax) = V2TH / 4 RL lub V2TH / 4 RTH

Dowód twierdzenia o maksymalnym przenoszeniu mocy

W niektórych zastosowaniach celem obwodu jest dostarczenie maksymalnej mocy do obciążenia. Kilka przykładów:

Wzmacniacze stereo
Nadajniki radiowe
Sprzęt komunikacyjny

Jeśli cały obwód zostanie zastąpiony jego równoważnym obwodem Thevenin, z wyjątkiem obciążenia, jak pokazano poniżej, moc pochłaniana przez obciążenie wynosi:

Dowód twierdzenia o maksymalnym przenoszeniu mocy

P._L= ja^dwaR_L= (V_th/ R_th+ R._L)^dwax R_L= V^dwa_thR_L/ (R_th+ R._L)^dwa

Ponieważ VTH i RTH są ustalone dla danego obwodu, moc obciążenia jest funkcją rezystancji obciążenia RL.

Rozróżniając PL względem RL i ustawiając wynik na zero, otrzymujemy następujące twierdzenie o przenoszeniu maksymalnej mocy Maksymalna moc występuje, gdy RL jest równe RTH.

Gdy spełniony jest warunek maksymalnego przekazania mocy, tj. RL = RTH, maksymalna przenoszona moc wynosi:

Zróżnicowanie PL względem RL

P._L= V^dwa_thR_L/ [R_th+ R._L]^dwa= V^dwa_thR_th/ [R_th+ R._L]^dwa= V^dwa_th/ 4 R_th

Kroki do rozwiązania twierdzenia o przenoszeniu maksymalnej mocy

Poniższe kroki służą do rozwiązania problemu za pomocą twierdzenia o maksymalnym przenoszeniu mocy

Krok 1: Usuń rezystancję obciążenia obwodu.

Krok 2: Znajdź rezystancję Thevenina (RTH) sieci źródłowej patrząc przez otwarte terminale obciążenia.

Krok 3: Zgodnie z twierdzeniem o maksymalnym przenoszeniu mocy, RTH to rezystancja obciążenia sieci, tj.RL = RTH, która umożliwia maksymalny transfer mocy.

Krok 4: Maksymalny transfer mocy jest obliczany za pomocą poniższego równania

(Pmax) = V2TH / 4 RTH

Twierdzenie o przenoszeniu maksymalnej mocy Przykładowe problemy z rozwiązaniami

Znajdź wartość RL dla poniższego obwodu, dla którego moc jest również najwyższa, znajdź najwyższą moc przez RL, korzystając z twierdzenia o maksymalnym przenoszeniu mocy.

Znajdowanie wartości RL

Rozwiązanie:

Zgodnie z tym twierdzeniem, gdy moc jest największa przez obciążenie, to opór jest podobny do równego oporu między dwoma końcami RL po jego wyeliminowaniu.

Tak więc, dla odkrycia rezystancji obciążenia (RL), musimy znaleźć równoważną rezystancję:

Więc,

Teraz, aby odkryć najwyższą moc poprzez rezystancję obciążenia RL, musimy odkryć wartość napięcia między obwodami VOC.

Dla powyższego obwodu zastosuj analizę siatki. Możemy dostać:

Zastosuj KVL dla pętli-1:

6-6I1-8I1 + 8I2 = 0

-14I1 + 8I2 = -6 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ (1)

Zastosuj KVL dla pętli-2:

-8I2-5I2-12I2 + 8I1 = 0

8I1-25I2 = 0 ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ (2)

Rozwiązując powyższe dwa równania, otrzymujemy

I1 = 0,524 A.

I2 = 0,167 A.

Teraz z obwodu Vo.c jest

VA-5I2- VB = 0

Vo.c / VAB = 5I2 = 5X0,167 = 0,835v

Stąd maksymalna moc przez rezystancję obciążenia (RL) wynosi

P max = V_OC^dwa/ 4R_L= (0,835 x 0,835) / 4 x 3,77 = 0,046 wata

Odkryj najwyższą moc, jaką można przesłać do rezystora obciążenia RL w poniższym obwodzie.

Maksymalna moc do RL

Rozwiązanie:

Zastosuj twierdzenie Thevenina do powyższego obwodu,

“zasilanie zmienne napięcie i prąd ”

Tutaj napięcie Thevenina (Vth) = (200/3) i rezystancja Thevenina (Rth) = (40/3) Ω

Zastąp ułamek obwodu, który znajduje się po lewej stronie zacisków A i B danego obwodu, zastępczym obwodem Thevenina. Schemat obwodu wtórnego pokazano poniżej.

Maksymalną moc, która zostanie dostarczona do rezystora obciążenia, RL, możemy znaleźć za pomocą następującego wzoru.

PL, Max = V2TH / 4 RTH

Podstaw VTh = (200/3) V i RTh = (40/3) Ω w powyższym wzorze.

PL, Max = (200/3)^dwa/ 4 (40/3) = 250/3 watów

Dlatego maksymalna moc, która zostanie dostarczona do rezystora obciążenia RL danego obwodu, wynosi 250/3 W.

Zastosowania twierdzenia o przenoszeniu maksymalnej mocy

Twierdzenie o maksymalny transfer mocy można zastosować na wiele sposobów w celu określenia wartości rezystancji obciążenia, która otrzymuje maksymalną moc z zasilacza i maksymalną moc w stanie największego transferu mocy. Poniżej znajduje się kilka zastosowań twierdzenia o maksymalnym przenoszeniu mocy:

To twierdzenie jest zawsze poszukiwane w systemie komunikacyjnym. Na przykład, w systemie adresowania społeczności, obwód jest dostrojony do najwyższego transferu mocy, dzięki czemu głośnik (rezystancja obciążenia) jest równoważny wzmacniaczowi (rezystancja źródła). Kiedy obciążenie i źródło są dopasowane, ma równy opór.
W silnikach samochodowych moc przekazywana do rozrusznika samochodowego będzie zależeć od efektywnej rezystancji silnika i wewnętrznego oporu akumulatora. Gdy te dwie rezystancje są równoważne, wówczas największa moc zostanie przekazana do silnika w celu uruchomienia silnika.

Chodzi o twierdzenie o maksymalnej mocy. Na podstawie powyższych informacji możemy wreszcie wywnioskować, że to twierdzenie jest często używane, aby zapewnić, że najwyższą moc można przesłać ze źródła mocy do obciążenia. Oto pytanie do ciebie, jaka jest zaleta twierdzenia o przenoszeniu maksymalnej mocy?