Matematyka odgrywa decydującą rolę w zrozumieniu zachowania i działania elektryczny i systemy elektroniczne . Wielomiany, algebra, prawdopodobieństwo, całkowanie i różniczkowanie itd.… Stanowią znaczną część narzędzi używanych do rozwiązywania układów. Wraz ze wzrostem złożoności systemów wymagane są bardzo wyrafinowane metody. Równania różniczkowe są często używane do definiowania systemów sterowania. Te równania są proste do rozwiązania. Ale złożoność pojawia się podczas rozwiązywania równań różniczkowych wyższego rzędu. Aby rozwiązać takie złożone równania różniczkowe wyższego rzędu, skuteczna okazała się metoda matematyczna Transformata Laplace'a . Ponieważ ta transformacja jest szeroko stosowana, warto wiedzieć, do czego naprawdę służyły i jak działają.
Co to jest transformata Laplace'a?
W matematyce transformacje są stosowane do przekształcania zmiennej z jednej postaci w inną, aby uczynić równanie łatwym w obsłudze. Transformacja Laplace'a robi prawie to samo. Przekształcają równanie różniczkowe wyższego rzędu w postać wielomianową, co jest o wiele łatwiejsze niż bezpośrednie rozwiązywanie równania różniczkowego.
Ale są różne transformacje, takie jak transformata Fouriera, transformaty z, co sprawia, że transformata Laplace'a jest wyjątkowa? Główną zaletą transformaty Laplace'a jest to, że są one definiowane zarówno dla stabilnych, jak i niestabilnych systemów, podczas gdy transformaty Fouriera są definiowane tylko dla stabilnych systemów.
Formuła transformacji Laplace'a
Transformacja Laplace'a funkcji f (t) w dziedzinie czasu, gdzie t jest liczbą rzeczywistą większą lub równą zeru, podaje się jako F (s), gdzie  s jest liczbą zespoloną w dziedzinie częstotliwości. tj. s = σ + jω
s jest liczbą zespoloną w dziedzinie częstotliwości. tj. s = σ + jω
Powyższe równanie jest uważane za jednostronny Równanie przekształcenia Laplace'a . Gdy granice zostaną rozszerzone na całą rzeczywistą oś, wtedy Dwustronna transformata Laplace'a można zdefiniować jako
 W praktycznych obwodach, takich jak Obwody RC i RL Zwykle używane są warunki początkowe, więc do analizy stosuje się jednostronne transformaty Laplace'a.
W praktycznych obwodach, takich jak Obwody RC i RL Zwykle używane są warunki początkowe, więc do analizy stosuje się jednostronne transformaty Laplace'a.
Jak s = σ + jω, gdy σ = 0 transformata Laplace'a zachowuje się jak transformata Fouriera.

Formuły transformacji Laplace'a
Warunki stosowalności transformaty Laplace'a
Transformaty Laplace'a nazywane są transformatami całkowitymi, więc istnieją niezbędne warunki dla zbieżności tych przekształceń.
 tj. f musi być lokalnie integrowalna dla przedziału [0, ∞) i zależnie od tego, czy σ jest dodatnie czy ujemne, e ^ (- σt) może zanikać lub rosnąć. W przypadku dwustronnych transformacji Laplace'a zamiast pojedynczej wartości całka zbiega się w pewnym zakresie wartości znanym jako Region zbieżności.
tj. f musi być lokalnie integrowalna dla przedziału [0, ∞) i zależnie od tego, czy σ jest dodatnie czy ujemne, e ^ (- σt) może zanikać lub rosnąć. W przypadku dwustronnych transformacji Laplace'a zamiast pojedynczej wartości całka zbiega się w pewnym zakresie wartości znanym jako Region zbieżności.
Właściwości transformaty Laplace'a:
Liniowość

Liniowość
Przesunięcie w czasie

Przesunięcie w czasie
Przesunięcie w domenie S.

Przesunięcie w domenie S.
Odwrócenie czasu

Odwrócenie czasu
Zróżnicowanie w domenie S.

Zróżnicowanie w domenie S.
Konwolucja w czasie

Konwolucja w czasie
Twierdzenie o wartości początkowej
Twierdzenie o wartości początkowej jest stosowane, gdy w transformacji Laplace'a stopień licznika jest mniejszy niż stopień mianownika  Twierdzenie o wartości końcowej:
Twierdzenie o wartości końcowej:
Jeśli wszystkie bieguny sF (s) leżą w lewej połowie płaszczyzny S, to stosuje się twierdzenie o wartości końcowej.
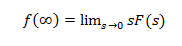 Odwrotna transformata Laplace'a
Odwrotna transformata Laplace'a
Ze względu na charakterystykę zbieżności transformata Laplace'a ma również transformację odwrotną. Przekształcenia Laplace'a wykazują odwzorowanie jeden do jednego z jednej przestrzeni funkcyjnej do drugiej. Wzór na odwrotną transformatę Laplace'a to
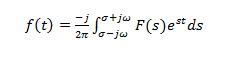 Jak obliczyć transformację Laplace'a?
Jak obliczyć transformację Laplace'a?
Przekształcenie Laplace'a sprawia, że równania są prostsze w obsłudze. Gdy podane jest równanie różniczkowe wyższego rzędu, stosowana jest do niego transformata Laplace'a, która przekształca równanie w równanie algebraiczne, ułatwiając w ten sposób obsługę. Następnie obliczamy pierwiastki przez uproszczenie tego równania algebraicznego. Teraz znajduje się odwrotna transformata Laplace'a prostszego wyrażenia, która rozwiązuje podane równanie różniczkowe wyższego rzędu.

Obliczanie transformacji Laplace'a
Zastosowania transformaty Laplace'a
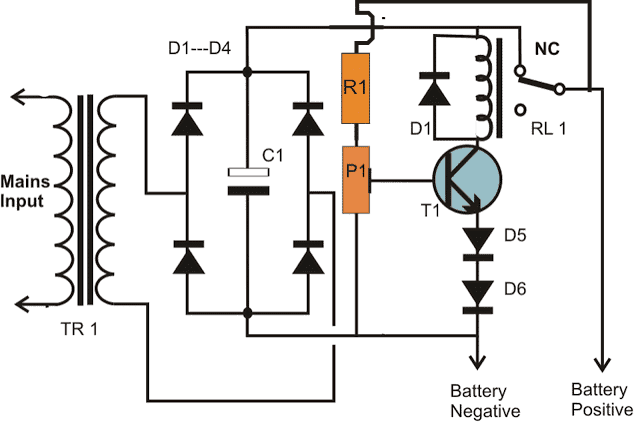
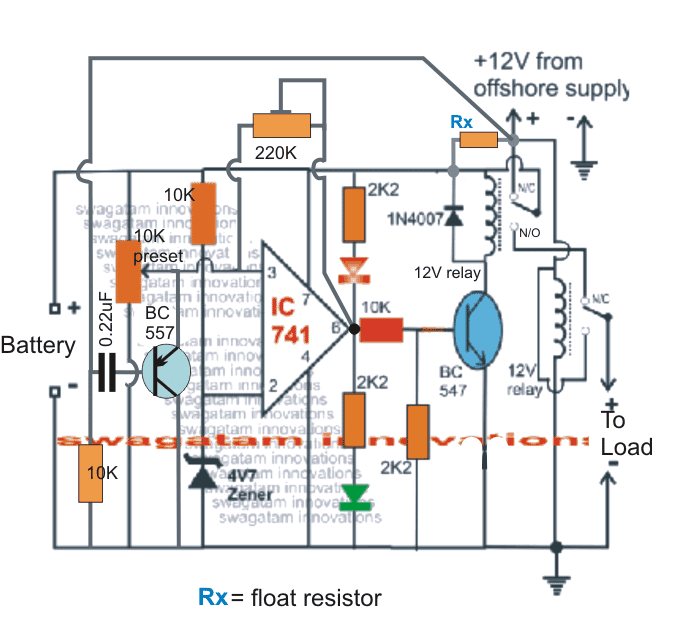
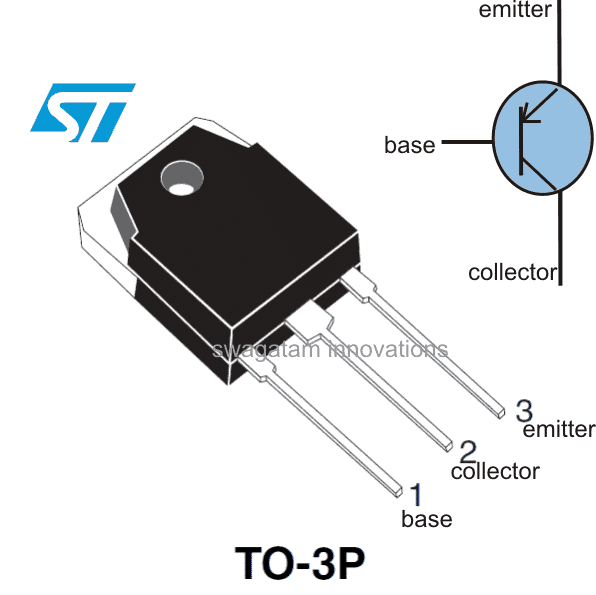
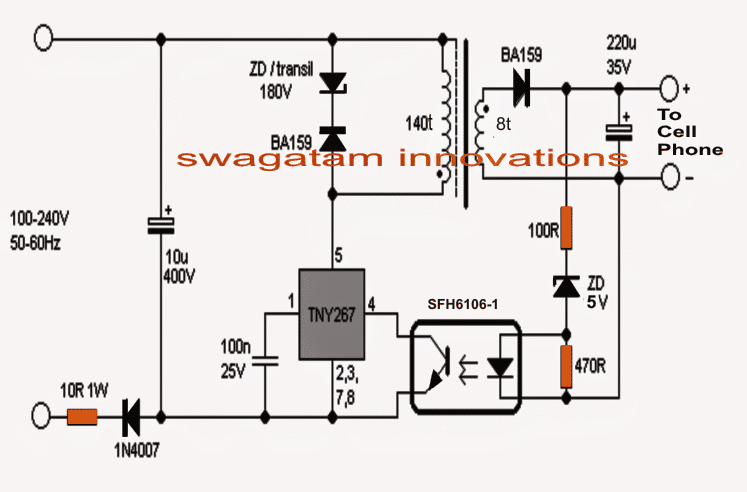
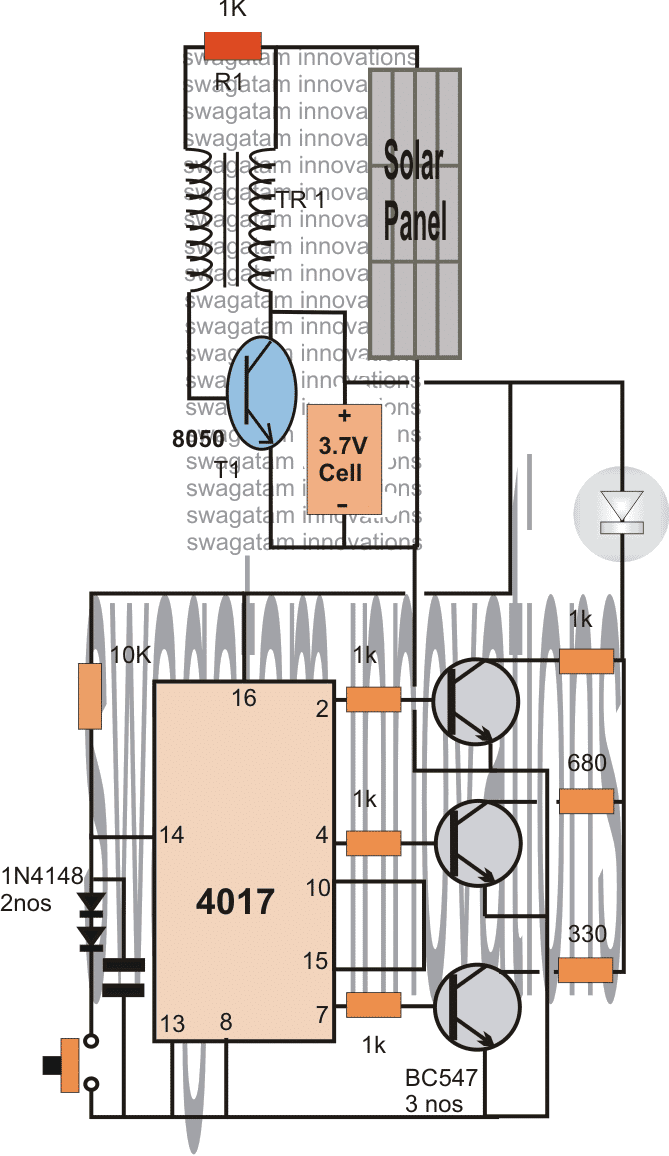
- Analiza elektryczna i elektroniczne obwody .
- Rozkładanie złożonych równań różniczkowych na prostsze formy wielomianowe.
- Przekształcenie Laplace'a dostarcza informacji o stanach ustalonych i przejściowych.
- W uczeniu maszynowym transformata Laplace'a jest używana do prognozowania i przeprowadzania analiz w eksploracji danych.
- Transformata Laplace'a upraszcza obliczenia w modelowaniu systemu.
Zastosowanie transformaty Laplace'a w przetwarzaniu sygnałów
Transformacje Laplace'a są często wybierane do przetwarzania sygnału. Wraz z transformacją Fouriera Transformata Laplace'a służy do badania sygnałów w dziedzinie częstotliwości. Gdy w sygnale występują małe częstotliwości w dziedzinie częstotliwości, można oczekiwać, że sygnał będzie gładki w dziedzinie czasu. Filtrowanie sygnału odbywa się zwykle w dziedzinie częstotliwości, w której Laplace działa jako ważne narzędzie do konwersji sygnału z domeny czasu do domeny częstotliwości.
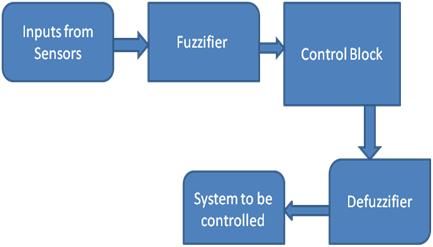
Zastosowanie transformaty Laplace'a w systemach sterowania
Systemy sterowania są zwykle zaprojektowane do kontrolowania zachowania innych urządzeń. Przykład systemy kontrolne może wahać się od prostego sterownika ogrzewania domu do przemysłowego systemu sterowania regulującego zachowanie maszyn.
Generalnie inżynierowie sterowania używają równań różniczkowych do opisania zachowania różnych bloków funkcjonalnych w pętli zamkniętej. Transformata Laplace'a jest tutaj używana do rozwiązywania tych równań bez utraty kluczowych informacji o zmiennych.
Charakterystyka liniowych układów niezmiennych w czasie z wykorzystaniem transformaty Laplace'a
Dla zwykłego systemu ROC związanego z systemem, funkcją jest prawa półpłaszczyzna. System jest anty-przypadkowy, jeśli jego odpowiedź impulsowa h (t) = 0 dla t> 0.
Jeśli ROC funkcji systemowych H (s) zawiera oś jω, to L.T.I. system nazywa się stabilnym systemem. Jeśli przypadkowy system z wymiernymi funkcjami systemu H (s) ma ujemne części rzeczywiste dla wszystkich swoich biegunów, to system jest stabilny.
Zatem transformata Laplace'a jest kluczowym narzędziem do analizy obwodów. Można powiedzieć, że stetoskop jest dla doktora Laplace'a, transformacje mają być inżynierem kontroli. Jak myślisz, za co przekształca Laplace? W jaki sposób były dla Ciebie pomocne?
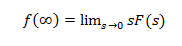 Odwrotna transformata Laplace'a
Odwrotna transformata Laplace'a 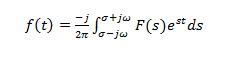 Jak obliczyć transformację Laplace'a?
Jak obliczyć transformację Laplace'a?