W obwodach kombinacyjnych różne bramki logiczne są używane do projektowania kodera, multipleksera, dekodera i demultipleksera. Obwody te mają pewne cechy, takie jak wyjście tego obwodu, zależy głównie od poziomów, które są obecne na zaciskach wejściowych w dowolnym momencie. Ten obwód nie zawiera żadnej pamięci. Wcześniejszy stan wejścia nie ma żadnego wpływu na aktualny stan tego obwodu. Wejścia i wyjścia obwodu kombinacyjnego to „n” nie. wejść & „m” nie. wyjść. Niektóre z obwodów kombinacyjnych to półsumatory i pełne sumatory, odejmowanie, koder, dekoder, multiplekser i demultiplekser. W tym artykule omówiono podsumowanie pół sumatora i pełnego sumatora oraz pracę z tabelami prawdy.
Co to jest adder?
Adder to plik cyfrowy obwód logiczny w elektronice, która jest szeroko stosowana do dodawania liczb. W wielu komputerach i innych typach procesorów sumatory są nawet używane do obliczania adresów i powiązanych działań oraz obliczania indeksów tabel w jednostce ALU, a nawet są wykorzystywane w innych częściach procesorów. Można je zbudować dla wielu reprezentacji liczbowych, takich jak nadmiar-3 lub dziesiętne kodowane binarnie. Sumatory są zasadniczo podzielone na dwa typy: Half Adder i Full Adder.
Co to jest obwód pół sumatora i obwód pełnego sumatora?
Obwód półsumatora ma dwa wejścia: A i B, które dodają dwie cyfry wejściowe i generują przeniesienie i sumę. Pełny obwód sumatora ma trzy wejścia: A i C, które dodają trzy liczby wejściowe i generują przeniesienie i sumę. Ten artykuł zawiera szczegółowe informacje o przeznaczeniu półsumatora i pełny dodatek w formie tabelarycznej, a nawet w schematach obwodów. Wspomniano już, że głównym i kluczowym celem dodatków jest dodawanie. Poniżej znajdują się szczegółowe informacje teoria pół sumatora i pełnego sumatora.

Basic Half Adder i Full Adder
Half Adder
Tak więc, dochodząc do scenariusza pół sumatora, dodaje dwie cyfry binarne, w których bity wejściowe są określane jako augend i addend, a wynikiem będą dwa wyjścia, jedno jest sumą, a drugie jest przenoszone. Aby wykonać operację sumowania, XOR jest stosowany do obu wejść, a bramka AND jest stosowana do obu wejść, aby wygenerować przeniesienie.

Schemat funkcjonalny HA
Podczas gdy w obwodzie pełnego sumatora dodaje 3 liczby jednobitowe, gdzie dwa z trzech bitów mogą być określane jako argumenty, a drugi jest określany jako przeniesione bity. Wytworzone wyjście jest 2-bitowe i można je odnieść jako przeniesienie produkcji i sumowanie.
Używając półsumatora, można zaprojektować prosty dodatek za pomocą bramek logicznych.
Zobaczmy przykład dodania dwóch pojedynczych bitów.
2-bitowy tabela prawdy półsumatora jest jak poniżej:

Tabela prawdy o połowie sumy
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
Są to najmniej możliwe kombinacje jednobitowe. Ale wynik dla 1 + 1 to 10, suma wyniku musi zostać ponownie zapisana jako 2-bitowe wyjście. W ten sposób równania można zapisać jako
0 + 0 = 00
0 + 1 = 01
1 + 0 = 01
1 + 1 = 10
Wynik „1” z „10” jest wykonany. „SUMA” to normalny wynik, a „PRZENIESIENIE” to wykonanie.
Teraz zostało wyjaśnione, że 1-bitowy sumator można łatwo zaimplementować za pomocą bramki XOR dla wyjścia „SUM” i bramki AND dla „Carry”.
Na przykład, gdy musimy dodać razem dwa 8-bitowe bajty, można to zaimplementować za pomocą obwodu logicznego z pełnym sumatorem. Półsumator jest przydatny, gdy chcesz dodać liczbę cyfr binarnych.
Sposobem na opracowanie dwucyfrowych sumatorów byłoby utworzenie tabeli prawdy i zmniejszenie jej. Jeśli chcesz utworzyć sumator z trzema cyframi binarnymi, operacja dodawania połowy sumatora jest wykonywana dwukrotnie. W podobny sposób decydując się na sumator czterocyfrowy, operacja jest wykonywana jeszcze raz. Dzięki tej teorii było jasne, że implementacja jest prosta, ale rozwój wymaga czasu.
Najprostsze wyrażenie używa wyłącznej funkcji LUB:
Suma = A XOR B.
Carry = A AND B

Schemat logiczny HA
Równoważnym wyrażeniem w zakresie podstawowego AND, OR i NOT jest:
SUMA = A.B + A.B ”
Kod VHDL dla Half Adder
Jednostka ha jest
Port (a: w STD_LOGIC
b: w STD_LOGIC
sha: out STD_LOGIC
cha: out STD_LOGIC)
koniec ha
Architektura Zachowanie powyższego obwodu jest
zaczynać
sha<= a xor b
Nie<= a and b
koniec Behawioralny
Połowa numeru IC Adder
Implementację półsumatora można przeprowadzić za pomocą cyfrowych układów scalonych o dużej szybkości CMOS, takich jak seria 74HCxx, która obejmuje SN74HC08 (7408) i SN74HC86 (7486).
Ograniczenia o połowę sumy
Głównym powodem nazywania tych sumatorów binarnych jak Half Adders jest to, że nie ma zakresu, w którym można by uwzględnić bit przenoszenia przy użyciu wcześniejszego bitu. Jest to więc główne ograniczenie HA, które kiedyś były używane jako sumator binarny, szczególnie w sytuacjach czasu rzeczywistego, które obejmują dodanie kilku bitów. Więc to ograniczenie można pokonać, używając pełnych sumatorów.
Pełny dodatek
Ten sumator jest trudny do zaimplementowania w porównaniu z pół-sumatorem.

Pełny schemat funkcjonalny dodatku
Różnica między półsumatorem a pełnym sumatorem polega na tym, że pełny sumator ma trzy wejścia i dwa wyjścia, podczas gdy półsumator ma tylko dwa wejścia i dwa wyjścia. Pierwsze dwa wejścia to A i B, a trzecie wejście jest przenoszone jako C-IN. Kiedy projektowana jest logika z pełnym sumowaniem, łączysz osiem z nich, aby utworzyć sumator o szerokości bajtów i kaskadowo przenosić bit z jednego sumatora do drugiego.

Tabela prawdy FA
Przenoszenie wyjścia jest oznaczone jako C-OUT, a normalne wyjście jest reprezentowane jako S, czyli „SUMA”.
Z powyższym pełna tabela prawdy sumatora implementację pełnego obwodu sumatora można łatwo zrozumieć. SUMA „S” jest tworzona w dwóch etapach:
- Poprzez XORowanie podanych danych wejściowych „A” i „B”
- Wynik A XOR B jest następnie XORowany za pomocą C-IN
To generuje SUMA i C-OUT jest prawdziwe tylko wtedy, gdy jedno z trzech wejść jest WYSOKIE, wtedy C-OUT będzie WYSOKIE. Tak więc możemy zaimplementować pełny obwód sumatora za pomocą dwóch obwodów półsumatorów. Początkowo sumator połówkowy zostanie użyty do dodania A i B w celu uzyskania częściowej sumy, a logika sumatora drugiej połowy może zostać użyta do dodania C-IN do sumy utworzonej przez sumator pierwszej połowy, aby uzyskać końcowe wyjście S.
Jeśli którakolwiek z logiki półsumatora generuje przeniesienie, pojawi się przeniesienie wyjściowe. Zatem C-OUT będzie funkcją OR półsumowanych wyjść Carry. Przyjrzyj się implementacji pełnego obwodu sumatora pokazanego poniżej.

Pełny diagram logiczny addera
Implementacja większych diagramów logicznych jest możliwa z powyższą logiką pełnego sumatora, a prostszy symbol jest najczęściej używany do reprezentowania operacji. Poniżej podano prostszą schematyczną reprezentację jednobitowego pełnego sumatora.
Za pomocą tego typu symbolu możemy dodać dwa bity razem, biorąc przeniesienie z następnego niższego rzędu wielkości i wysyłając przeniesienie do następnego wyższego rzędu wielkości. Na komputerze w przypadku operacji wielobitowych każdy bit musi być reprezentowany przez pełny sumator i musi być dodawany jednocześnie. Tak więc, aby dodać dwie liczby 8-bitowe, potrzebujesz 8 pełnych sumatorów, które można utworzyć przez kaskadowanie dwóch z 4-bitowych bloków.
Half Adder i Full Adder przy użyciu K-Map
Nawet sumę i wyniki przenoszenia dla połowy sumatora można również uzyskać metodą mapy Karnaugha (mapa K). Plik pół sumator i pełne wyrażenie logiczne sumatora można uzyskać za pomocą K-map. Tak więc mapa K dla tych sumatorów została omówiona poniżej.
Mapa K półsumatora to

Mapa HA K.
Pełny dodatek K-Map to

FA K-Map
Logiczne wyrażenie sumy i przenoszenia
Logiczne wyrażenie sumy (S) można określić na podstawie danych wejściowych wymienionych w tabeli.
= A’B’Cin + A ’B CCin’ + A B’Cin ’+ AB Cin
= Cin (A’B ’+ AB) + Cin’ (A’B + A B ’)
= Cin EX-OR (A EX-OR B)
= (1, 2, 4, 7)
Logiczne wyrażenie przeniesienia (Cout) można określić na podstawie danych wejściowych wymienionych w tabeli.
= A’B Cin + AB’Cin + AB Cin ’+ ABCin
= AB + BCin + ACin
= (3, 5, 6, 7)
Dzięki powyższym tabelom prawdy można uzyskać wyniki, a procedura jest następująca:
Obwód kombinacyjny łączy różne bramki w obwodzie, gdzie mogą to być koder, dekoder, multiplekser i demultiplekser . Charakterystyki obwodów kombinacyjnych są następujące.
- Wyjście w dowolnym momencie opiera się tylko na poziomach obecnych na zaciskach wejściowych.
- Nie używa żadnej pamięci. Poprzedni stan wejścia nie ma żadnego wpływu na aktualny stan obwodu.
- Może mieć dowolną liczbę wejść i m liczbę wyjść.
Kodowanie VHDL
Kodowanie VHDL dla pełnego dodatku obejmują następujące elementy.
encja full_add to
Port (a: w STD_LOGIC
b: w STD_LOGIC
cin: w STD_LOGIC
suma: out STD_LOGIC
cout: out STD_LOGIC)
koniec full_add
Architektura Zachowanie full_add to
składnik ha jest
Port (a: w STD_LOGIC
b: w STD_LOGIC
sha: out STD_LOGIC
cha: out STD_LOGIC)
komponent końcowy
sygnał s_s, c1, c2: STD_LOGIC
zaczynać
HA1: mapa portów ha (a, b, s_s, c1)
HA2: mapa portu ha (s_s, cin, sum, c2)
koszt<=c1 or c2
koniec Behawioralny
Plik różnica między sumatorem połowicznym a sumatorem pełnym polega na tym, że pół sumatora daje wyniki, a pełny sumator używa połowy sumatora do uzyskania innego wyniku. Podobnie, podczas gdy Full-Adder składa się z dwóch Half-Adderów, Full-Adder jest faktycznym blokiem, którego używamy do tworzenia obwodów arytmetycznych.
Carry Lookahead Adders
W koncepcji obwodów sumatora przenoszenia tętnienia bity niezbędne do dodania są natychmiast dostępne. Podczas gdy każda sekcja sumująca musi zachować swój czas na nadejście przeniesienia z poprzedniego bloku sumatora. Z tego powodu generowanie SUMA i PRZENOSZENIA zajmuje więcej czasu, ponieważ każda sekcja w obwodzie czeka na nadejście sygnału wejściowego.
Na przykład, aby dostarczyć dane wyjściowe dla n-tego bloku, musi otrzymać dane wejściowe z (n-1)-tego bloku. I to opóźnienie jest odpowiednio określane jako opóźnienie propagacji.
Aby przezwyciężyć opóźnienie w sumatorze przenoszenia tętnień, wprowadzono sumator przenoszenia z wyprzedzeniem. Tutaj za pomocą skomplikowanego sprzętu można zminimalizować opóźnienie propagacji. Poniższy diagram przedstawia sumator przenoszenia z wyprzedzeniem z pełnymi sumatorami.

Carry Lookahead przy użyciu pełnego sumatora
Tabela prawdy i odpowiadające jej równania wyjściowe to
| DO | b | do | C + 1 | Stan: schorzenie |
| 0 | 0 | 0 | 0 | No Carry Generować |
| 0 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 1 | No Carry Propagować |
| 1 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | Nieść Generować |
| 1 | 1 | 1 | 1 |
Równanie propagacji przenoszenia to Pi = Ai XOR Bi, a generowanie przeniesienia to Gi = Ai * Bi. Dzięki tym równaniom równania sumy i przenoszenia można przedstawić jako
SUMA = Pi XOR Ci
Ci + 1 = Gi + Pi * Ci
Gi zapewnia przenoszenie tylko wtedy, gdy oba wejścia Ai i Bi mają wartość 1, bez uwzględnienia przenoszenia wejściowego. Pi jest związane z propagacją przenoszenia od Ci do Ci + 1.
Różnica między Half Adder i Full Adder
Plik różnica między pół sumatorem a pełną tabelą sumatora pokazano poniżej.
| Half Adder | Pełny dodatek |
| Half Adder (HA) to kombinacyjny obwód logiczny, który służy do dodawania dwóch jednobitowych cyfr. | Full Adder (FA) to obwód kombinacyjny, który służy do dodawania trzech jednobitowych cyfr. |
| W HA po wygenerowaniu przeniesienia z poprzedniego dodania nie można dodać do następnego kroku. | W FA, po wygenerowaniu przeniesienia z wcześniejszego dodania, można go dodać do następnego kroku. |
| Pół sumator zawiera dwie bramki logiczne, takie jak bramka AND i bramka EX-OR. | Pełny dodatek zawiera dwie bramki EX-OR, dwie bramki OR i dwie bramki AND. |
| Bity wejściowe w półsumatorze to dwa, takie jak A, B. | Bity wejściowe w pełnym sumatorze to trzy, takie jak A, B i C-in |
| Połowa sumy sumy i równanie przeniesienia to S = a⊕b C = a * b | Pełne wyrażenie logiczne sumatora to S = a ⊕ b⊕Cin Cout = (a * b) + (Cin * (a⊕b)). |
| HA znajduje zastosowanie w komputerach, kalkulatorach, urządzeniach służących do pomiarów cyfrowych itp. | FA jest używany w procesorach cyfrowych, dodawaniu wielu bitów itp. |
Plik kluczowe różnice między pół sumatorem i pełnym sumatorem omówiono poniżej.
- Połowa sumatora generuje sumę i przeniesienie, dodając dwa wejścia binarne, podczas gdy pełny sumator jest używany do generowania sumy i przenoszenia przez dodanie trzech wejść binarnych. Architektura sprzętowa półsumatora i pełnego sumatora nie jest taka sama.
- Główną cechą, która odróżnia HA i FA jest to, że w HA nie ma takiej umowy, która uwzględniałaby ostatni dodatek przenoszący jako jego dane wejściowe. Ale FA lokalizuje określoną kolumnę wejściową, taką jak Cin, aby uwzględnić bit przenoszenia ostatniego dodatku.
- Dwa sumatory pokażą różnicę w oparciu o komponenty użyte w obwodzie do jego budowy. Półsumatory (HA) są zaprojektowane z połączeniem dwóch bramek logicznych, takich jak AND i EX-OR, podczas gdy FA jest zaprojektowany z kombinacją trzech bramek AND, dwóch XOR i jednej OR.
- Zasadniczo HA działają na 2 lub dwóch wejściach 1-bitowych, podczas gdy FA działają na trzech wejściach 1-bitowych. Półsumator jest używany w różnych urządzeniach elektronicznych do oceny dodawania, podczas gdy pełny sumator jest używany w procesorach cyfrowych do dodawania długiego bitu.
- Podobieństwa w tych dwóch sumatorach są takie, że oba HA i FA są kombinowanymi obwodami cyfrowymi, więc nie używają żadnego elementu pamięci, takiego jak układy sekwencyjne. Obwody te są niezbędne do wykonywania operacji arytmetycznych w celu dodania liczby binarnej.
Pełna implementacja adderów przy użyciu półsumatorów
Implementację FA można przeprowadzić za pomocą dwóch półsumatorów, które są połączone logicznie. Schemat blokowy tego można pokazać poniżej, który mówi o połączeniu FA za pomocą dwóch półsumatorów.
Suma i przeniesienie równań z poprzednich obliczeń to
S = A „B” Cin + A „BC” in + ABCin
Cout = AB + ACin + BCin
Równanie sumaryczne można zapisać jako.
Cin (A’B ‘+ AB) + C’ in (A ’B + A B’)
Więc suma = Cin EX-OR (A EX-OR B)
Cin (A EX-OR B) + C’in (A EX-OR B)
= Cin EX-OR (A EX-OR B)
Cout można zapisać w następujący sposób.
COUT = AB + ACin + BCin.
Cout = AB + + rozczarowanie BCIN (a + a)
= ABCin + AB + ACin + A ’B Cin
= AB (1 + Cin) + ACin + A ’B Cin
= A B + ACin + A ’B Cin
= AB + ACin (B + B ’) + A’ B Cin
= ABCin + AB + A’B Cin + A ’B Cin
= AB (Cin + 1) + A B Cin + A ’B Cin
= AB + AB ’Cin + A’ B Cin
= AB + Cin (AB ’+ A’B)
Dlatego COUT = AB + Cin (A EX-OR B)
W zależności od powyższych dwóch równań sum i przenoszenia, obwód FA można zaimplementować za pomocą dwóch HA i bramki OR. Schemat obwodu pełnego sumatora z dwoma półsumatorami pokazano powyżej.

Pełny sumator przy użyciu dwóch półsumatorów
Pełny projekt dodatku z użyciem bramek NAND
Bramka NAND to jedyny rodzaj bramki uniwersalnej, używanej do wykonywania dowolnego projektu logicznego. Obwód FA ze schematem bramek NAND pokazano poniżej.

FA przy użyciu bramek NAND
FA jest łatwym jednobitowym sumatorem i jeśli chcemy wykonać dodawanie n-bitów, to n nie. jednobitowych FA musi być zastosowanych w formacie połączenia kaskadowego.
Zalety
Plik zalety półsumatora i pełnego sumatora obejmują następujące elementy.
- Głównym celem półsumatora jest dodanie dwóch liczb jednobitowych
- Pełne sumatory posiadają możliwość dodania przenoszonego bitu, który jest wynikiem poprzedniego dodania
- Dzięki pełnemu sumatorowi można zaimplementować kluczowe obwody, takie jak sumator, multiplekser i wiele innych
- Pełne obwody sumatora zużywają minimalną moc
- Zaletą pełnego sumatora w stosunku do pół sumatora jest to, że pełny sumator jest używany w celu wyeliminowania wady pół sumatora, ponieważ pół sumator jest używany głównie do dodawania dwóch liczb 1-bitowych. Połówki sumatorów nie dodają przenoszonego bitu, więc do pokonania tego pełnego sumatora jest używany. W pełnym sumatorze można dodać trzy bity i generuje dwa wyjścia.
- Projektowanie dodatków jest proste i jest to podstawowy element składowy, dzięki któremu można łatwo zrozumieć jednobitowe dodawanie.
- Ten sumator można przekształcić w pół odejmowanie, dodając falownik.
- Dzięki zastosowaniu pełnego sumatora można uzyskać wysoką wydajność.
- Wysoka prędkość
- Bardzo mocne do skalowania napięcia zasilania
Niedogodności
Plik wady pół sumatora i pełnego sumatora obejmują następujące elementy.
- Ponadto pół sumatora nie można użyć przed przenoszeniem, więc nie ma zastosowania do kaskadowego dodawania wielobitowego.
- Aby przezwyciężyć tę wadę, w FA konieczne jest dodanie trzech 1 bitów.
- Gdy FA jest używany w postaci łańcucha, takiego jak RA (Ripple Adder), można zmniejszyć zdolność wyjściową napędu.
Aplikacje
Zastosowania pół sumatora i pełnego sumatora obejmują następujące elementy.
- Dodawanie bitów binarnych można wykonać za pomocą pół sumatora za pomocą jednostki ALU w komputerze, ponieważ używa ona sumatora.
- Do zaprojektowania pełnego obwodu sumatora można użyć kombinacji połowy sumatora.
- Półsumatory są używane w kalkulatorach i do pomiaru adresów oraz tabel
- Te obwody są używane do obsługi różnych aplikacji w obwodach cyfrowych. W przyszłości odgrywa kluczową rolę w elektronice cyfrowej.
- Obwód FA jest używany jako element w wielu dużych obwodach, takich jak Ripple Carry Adder. Ten sumator dodaje jednocześnie liczbę bitów.
- FA są używane w jednostce arytmetycznej (ALU)
- FA są używane w aplikacjach związanych z grafiką, takich jak GPU (Graphics Processing Unit)
- Są one używane w obwodzie mnożenia do wykonywania mnożenia Carryout.
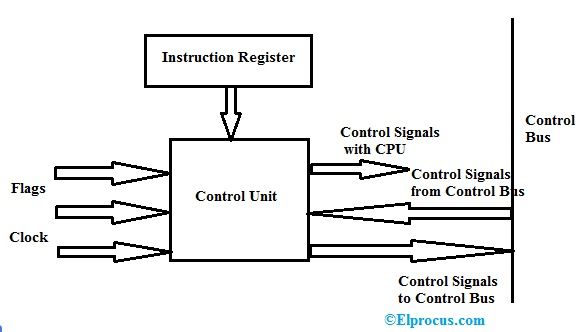
- W komputerze do wygenerowania adresu pamięci i zbudowania kontrapunktu programu w kierunku kolejnej instrukcji używana jest jednostka arytmetyczno-logiczna za pomocą pełnych sumatorów.
Tak więc, ilekroć dodawane są dwie liczby binarne, cyfry są dodawane najpierw na najmniejszych bitach. Ten proces można wykonać za pomocą półsumatora, ponieważ najprostszy n / w, który umożliwia dodanie dwóch liczb 1-bitowych. Wejścia tego sumatora to cyfry binarne, podczas gdy wyjścia to suma (S) i przeniesienie (C).
Ilekroć uwzględniana jest liczba cyfr, wówczas sieć HA jest wykorzystywana po prostu do łączenia najmniejszych cyfr, ponieważ HA nie może dodać numeru przeniesienia z wcześniejszej klasy. Pełny sumator można zdefiniować jako podstawę wszystkich cyfrowych urządzeń arytmetycznych. Służy do dodawania trzech liczb 1-cyfrowych. Ten sumator zawiera trzy wejścia, takie jak A, B i Cin, podczas gdy wyjścia to Sum i Cout.
Powiązane pojęcia
Plik pojęcia związane z pół sumatorem i pełnym sumatorem po prostu nie trzymaj się jednego celu. Mają szerokie zastosowanie w wielu aplikacjach, a kilka z nich jest wymienionych:
- Pół sumatora i pełny numer IC sumatora
- Opracowanie 8-bitowego dodatku
- Jakie są środki ostrożności dotyczące połowy sumy?
- Aplet JAVA dodatku Ripple Carry
Dlatego chodzi o teoria pół sumatora i pełnego sumatora wraz z tabelami prawdy i diagramami logicznymi pokazano również projekt pełnego sumatora wykorzystującego obwód półsumatora. Wiele z pół sumatora i pełny dodatek pdf dostępne są dokumenty zawierające zaawansowane informacje o tych pojęciach. Ponadto ważne jest, aby wiedzieć jak zaimplementowano 4-bitowy pełny sumator ?